处理布尔查询
我们如何使用 inverted index 以及基础的布尔检索模型来处理查询呢?考虑以下查询:
(A) Brutus AND Calpurnia
我们分为以下几个步骤:
- 在字典中定位 Brutus。
- 获取它的 postings。
- 在字典中定位 Calpurnia。
- 获取它的 postings。
- 对这两个 postings lists 进行 intersect 操作,如 figure 1.5 所示的那样。
这里 intersection 操作很关键:我们需要很高效的 intersection,进而很快地定位到有共同词组的文档。(有时候这个操作也被称为 merging postings lists,熟悉 merge sort 的朋友可以类比一下)。

Figure:Intersecting the postings lists for Brutus and Calpurnia from Figure 1.3
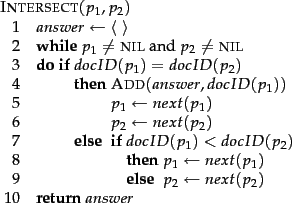
Figure 1.6: Algorithm for the intersection of two postings lists .
有一个简单并且高效的方法来 intersect postings lists,就是 merge algorithm(见 Figure 1.6):我们维护指向 lists 的指针,并且同时遍历两个 postings lists,总的是线性的时间开销。在每一步,我们比较指针所指的 docID,如果它们相同,就把那个 docID 存入 results list,并且两个指针都向前一步。不相同的话,我们把指向较小 docID 的指针向前一步,如果 postings lists 的长度分别是 x 和 y,那么 intersect 需要 O(x+y) 操作。更准确来说,查询的时间复杂度是 , N 是 collection 中 documents 的数量。要有效使用这个算法,关键是 postings be sorted by a single global ordering,直接通过 docID 的数字来排序是一种作法。
我们可以把 intersection operation 扩展来处理更为复杂的查询,比如说:
(Brutus OR Caesar) AND NOT Calpurnia
查询的优化是指在处理查询的过程中,如何组织具体的执行,从而使得系统只需要最少的工作量。对于布尔查询而言,一个相关的例子就是访问 postings lists 的顺序,以下查询该以什么顺序执行呢?
Brutus AND AND Calpurnia
对于每一个 t terms,我们需要获取它的 postings,然后把它们 AND 在一起。一个比较主观的作法就是以 increasing document frequency 的顺序来处理:如果我们先 intersecting 两个最小的 postings lists,那么这个中间的结果一定没有这两个大,我们可能就能减少很大的工作量。对 Figure 1.3,我们以这样的顺序执行:
(Calpurnia AND Brutus) AND Caesar
这是第一次明确说明,为什么要存储 frequency of terms:它让我们能够在 in-memory 数据上进行排序。
下面考虑更为广泛的优化,例如:
(madding OR crowd) AND (ignoble OR strife) AND (killed OR slain)
和之前一样,我们先获取所有 terms 的frequencies,然后可以估计每个 OR 操作所得的结果的大致大小,就是 frequencies of disjuncts 的和。之后再以 increasing order 来进行处理。

Figure 1.7: Algorithm for conjunctive queries that returns the set of documents containing each term in the input list of terms.
对于任意的布尔查询,复杂的语句要先暂存中间结果再进行处理。然而在很多时候,可能是因为查询语言本身的特点,或者是因为用户提交的查询是最为普遍的一种,a query is purely conjunctive。在这种情况下,更为有效的是对每个获取的 postings list 和当前在内存中的中间结果进行 intersect 操作,而不是把 merging 当作是对于两个输入以及一个单一输出的一种函数。这里我们通过读取 postings list of the least frequent term 来初始化中间结果。这个算法如 Figure 1.7 所示,这里的 intersection 操作是不对称的:中间结果的 list 是在内存中的,而另一个要操作的 list 却是要被从硬盘中读取的。更进一步而言,中间结果的 list 总是至少和另一个 list 一样长的,and in many cases it is orders of magnitude shorter。 postings 的 intersection 还是可以使用 Figure 1.6 的算法来处理,但是当 list lengths 的差距非常巨大的时候,其他的优化技术就有一展身手的时机了。